「SPOJ 1043」GSS1 - Can you answer these queries I

Description

给定一个长度为 $n\ (n \leq 50000, \mid a_i \mid \leq 15007)$ 的整数序列，对于 $m\ (m \leq 50000)$ 个询问 $l,r\ (1 \leq l \leq r \leq n)$，求区间 $[l,r]$ 的最大子段和。

Source

[Luogu]SP1043

[SPOJ]GSS1

Solution

前置知识：

线段树

如果用朴素的最大子段和算法，时间复杂度为 $O(nm)$，一定会超时。

很容易想到用数据结构来维护。

我们建立一棵线段树，对于区间 $x$，有以下定义：

$sum[x]$ 表示区间和；

$lsum[x]$ 表示以该区间左端点为起点的最大子段和；

$rsum[x]$ 表示以该区间右端点为起点的最大子段和；

$res[x]$ 表示该区间内的最大子段和。

与普通的线段树不同，这道题维护的信息很多，我们先来分析该题最重要的 $\mathrm{pushUp}$ 与 $\mathrm{query}$ 操作。

$\mathrm{pushUp}$ 操作

首先，是维护区间和，最基本的线段树操作，就不用多说了：

$$\large{sum[x] = sum[lson(x)] + sum[rson(x)]}$$

其次，假如我们知道一个区间的左右子区间信息，如何更新该区间的最大子段和？

很显然，答案可能为 左区间的最大子段和 或 右区间的最大子段和 。

除此之外，合并区间后，答案也有可能为 左区间的右起最大子段和 + 右区间的左起最大子段和，如上图。

由此我们可以得到代码：

$$\large{res[x]=\max\begin{Bmatrix}res[lson(x)],res[rson(x)],rsum[lson(x)]+lsum[rson(x)]\end{Bmatrix}}$$

那如何更新该区间的 左起最大子段和 和 右起最大子段和 呢？

区间左起最大子段和可以是 左区间的左起最大子段和 或 左区间的区间和 + 右区间的左起最大子段和，如上图。

右起最大子段和将上述操作反过来即可。

代码实现如下：

$$\large{\begin{aligned} lsum[x]&=\max(lsum[lson],sum[lson]+lsum[rson])\\[2ex] rsum[x]&=\max(rsum[rson],rsum[lson]+sum[rsum]) \end{aligned}}$$

$\mathrm{query}$ 操作

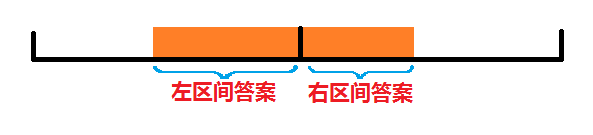
当答案来自两个不同的区间时（如图），我们需要对这两个区间答案进行合并，并不只是取最大值那样简单。

我们还需要进行类似 $\mathrm{pushUp}$ 的操作，已知左右区间的答案，更新该区间答案。

函数的返回值有很多，所以用结构体式线段树实现更方便。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

template <class T>
inline void read(T &x) {
    x = 0;
    char c = getchar();
    bool f = 0;
    for (; !isdigit(c); c = getchar()) f ^= c == '-';
    for (; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
    x = f ? -x : x;
}

template <class T>
inline void write(T x) {
    if (x < 0) {
        putchar('-');
        x = -x;
    }
    T y = 1;
	int len = 1;
    for (; y <= x / 10; y *= 10) ++len;
    for (; len; --len, x %= y, y /= 10) putchar(x / y + 48);
}

const int MAXN = 5e4 + 10;
int n, q, l, r;
LL a[MAXN];
struct SegmentTree {
    struct Node {
        LL sum, lsum, rsum, res;
    } seg[MAXN << 2];
    
    inline int lson(int x) {
        return x << 1;
    }
    inline int rson(int x) {
        return x << 1 | 1;
    }
    inline Node merge(Node x, Node y) {
        Node now;
        now.sum = x.sum + y.sum;
        now.res = max(max(x.res, y.res), x.rsum + y.lsum);
        now.lsum = max(x.lsum, x.sum + y.lsum);
        now.rsum = max(y.rsum, x.rsum + y.sum);
        return now;
    }
    inline void pushUp(int x) {
        seg[x] = merge(seg[lson(x)], seg[rson(x)]);
    }
    void build(int x, int l, int r, LL *a) {
        if (l == r) {
            seg[x] = (Node) { a[l], a[l], a[l], a[l] };
            return;
        }
        int mid = (l + r) >> 1;
        build(lson(x), l, mid, a), build(rson(x), mid + 1, r, a);
        pushUp(x);
    }
    Node query(int ql, int qr, int l, int r, int x) {//分成 3 种情况考虑
        if (ql <= l && qr >= r) return seg[x];
        int mid = (l + r) >> 1;
        if (qr <= mid) return query(ql, qr, l, mid, lson(x));
        if (ql > mid) return query(ql, qr, mid + 1, r, rson(x));
        return merge(query(ql, qr, l, mid, lson(x)), 
        query(ql, qr, mid + 1, r, rson(x)));
    }
} tr;

int main() {
    read(n);
    for (int i = 1; i <= n; ++i) read(a[i]);
    tr.build(1, 1, n, a);
    for (read(q); q; --q) {
        read(l), read(r);
        write(tr.query(l, r, 1, n, 1).res);
        putchar('\n');
    }
    return 0;
}