「Luogu P4284」「SHOI2014」概率充电器

Description

给定一棵 $n$ 个点的树，每个节点都有一个充电元件，第 $i$ 条边有 $p_i \%$ 的概率导电，第 $i$ 个点有 $q_i \%$ 的概率充电。求期望通电的元件个数，保留 $6$ 位小数。

Source

[Luogu]P4284

Solution

首先根据 期望 的性质：

$$\large { E(A + B) = E(A) + E(B) }$$

得到

$$\large {\begin{aligned} E\left( \sum\limits_{i=1}^n i \right) = \sum\limits_{i=1}^nE(i) = \sum\limits_{i=1}^n p_ix_i \end{aligned}}$$

因为每个充电元件的贡献都是 $1$（即 $x_i = 1$），所以问题就是求所有元件充电的概率总和：

$$\large { \sum\limits_{i=1}^n p_i }$$

其中 $p_i$ 是元件 $i$ 通电的概率。这个东西怎么求呢？尝试 树形DP 。

状态：

用 $p_u$ 表示元件 $u$ 通电的概率。

转移：

考虑节点 $u$ 通电的 $3$ 种可能：

1. 节点 $u$ 自己充电；
2. 子树里有一个节点充电并传导到节点 $u$；
3. 子树外有一个节点充电并传导到节点 $u​$ 。

节点 $u$ 自己充电很好实现，因为节点 $u$ 通电的初始概率就是读入进来的 $p_u$ 。

但是后两种似乎很难同时实现，干脆分两次 $\rm{dfs}​$ 解决。

对于第一次 $\rm{dfs}​$，我们先考虑第二种可能，有以下方程

$$\large {\begin{aligned} & p_u = p_u \cup \left( p_v \times q_{u \rightarrow v} \right) & \left( v \in son_u\right) \end{aligned}}$$

其中 $q_{u \rightarrow v}​$ 表示边 $u \rightarrow v​$ 导电的概率。节点 $u​$ 通电的概率就是 节点 $u​$ 自己发电 与 子节点 $v​$ 通电后经过边 $u \rightarrow v​$ 传导到 $u​$ 的并集，换句话说，就是上述两种情况至少发生一种的概率。两个概率的并怎么求呢？有如下公式

$$\large { \begin{aligned} P\left( A \cup B \right) &= P\left( A \right) + P\left( B \right) - P\left( A \cap B \right)\\ &= P\left( A \right) + P\left( B \right) - P\left( A \right) \times P\left( B \right) \end{aligned} }$$

很好证明，因为 $A$ 和 $B$ 至少发生一种，分 $3$ 种情况讨论（都运用了 乘法原理）：

1. $A​$ 发生 $B​$ 不发生，概率为 $P\left(A \right) \times \left( 1 - P \left( B\right) \right)​$；
2. $B$ 发生 $A$ 不发生，概率为 $P\left(B \right) \times \left( 1 - P \left( A\right) \right)$ ；
3. $A​$ 与 $B​$ 同时发生，概率为 $P \left( A\right) \times P \left( B\right)​$ 。

根据 加法原理，把上述值加起来即能得证。这样我们就处理好了子树里节点导电的情况。

对于第二次 $\rm{dfs}​$，我们再考虑第三种可能，有以下方程

$$\large {\begin{aligned} & p_v = p_v \cup \left( \frac{p_u - p_v \times q_{u \rightarrow v}}{1 - p_v \times q_{u \rightarrow v}} \times q_{u \rightarrow v} \right) & \left( v \in son_u\right) \end{aligned}}$$

其中 $q_{u \rightarrow v}$ 表示边 $u \rightarrow v$ 导电的概率。显然根节点（$root$）通电的概率已知（不可能有第三种可能），考虑通过父节点 $u$ 状态确定子节点 $v$ 。

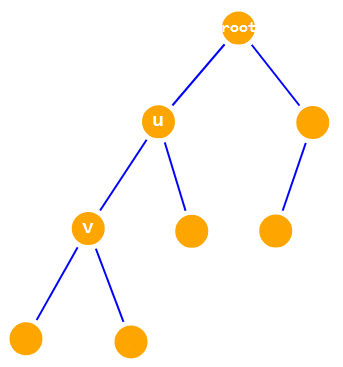
$p_v$ 的值一定为 当前 $p_v$ 的值（自己和子树内的通电概率） 和 子树外节点通电传导给 $v$ 的并。其中 $v$ 子树里的节点通电传导给 $u$ 的概率为 $p_v \times q_{u \rightarrow v}$，这个值与子节点 $v$ 的 子树外节点通电传导给 $u$ 的概率 的并是 $p_u$ 。而现在要求 子树外节点通电传导给 $u$ 的概率 。

这个问题可以转化为——若已知 $P \left( B\right),P \left( C\right)$ 的值，且 $P\left( A \cup B \right) = P \left ( C\right)$，怎么求 $P \left( A \right)$？

用刚才的公式倒推即可：

$$\large { P \left( A \cup B\right) = P \left( C \right) }$$ $$\large { P\left( A \right) + P\left( B \right) - P\left( A \right) \times P\left( B \right) = P\left( C \right) }$$ $$\large { P\left( A \right) - P\left( A \right) \times P\left( B \right) = P\left( C \right) -P\left( B \right) }$$ $$\large { P\left( A \right) \times \left( 1 - P\left( B \right) \right) = P\left( C \right) -P\left( B \right) }$$ $$\large {\begin{aligned} & P\left( A \right) = \frac{P\left( C \right) -P\left( B \right)}{1 - P\left( B \right)} & \left( P \left( B \right) \neq 1 \right) \end{aligned} }$$

根据这个式子求出 子树外节点通电传导给 $u$ 的概率，乘上 $q_{u \rightarrow v}$ 就是 子树外节点通电传导给 $v$ 的概率 了，再求 $p_v$ 与它的并，就是这个状态的值。值得注意的是，如果上述式子中的 $P\left( B \right) = 1$（即 $p_v \times q_{u \rightarrow v} = 1$），显然是不能直接除的，但因为 $0 \leq p_v,q_{u \rightarrow v} \leq 1$，所以 $p_v = q_{u \rightarrow v} = 1$，在这种情况下可以直接跳过，不进行转移（$p_v$ 一定通电）。最后把所有节点通电的概率加起来即为答案。

与第一次 $\rm{dfs}$ 不同的是：第一次是由子树合并答案，需要递归到底，返回时再转移；第二次是由父节点更新答案，遍历完整棵树即可。时间复杂度为 $O(n)​$ 。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

template <class T>
inline void read(T &x) {
    x = 0;
    char c = getchar();
    bool f = 0;
    for (; !isdigit(c); c = getchar()) f ^= c == '-';
    for (; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
    x = f ? -x : x;
}

const int MAXN = 5e5, MAXM = 5e5;
const double eps = 1e-7;
int n, tot, head[MAXN + 5];
double ans, p[MAXN + 5], x[MAXN + 5];
struct Edge {
    int next, to;
    double dis;
} e[(MAXM << 1) + 5];

inline void addEdge(int u, int v, double w) {
    e[++tot] = (Edge) { head[u], v, w };
    head[u] = tot;
}

inline double cup(double a, double b) {//求两个概率的并 a∪b
    return a + b - a * b;
}

inline double calc(double a, double b) {//已知 P(b) 以及 P(a)∪P(b)，求 P(a)
    return (a - b) / (1.0 - b);
}

void dfsUp(int u, int fa) {//第一次 dfs，子树内节点传导电
    for (int v, i = head[u]; v = e[i].to, i; i = e[i].next) {
        if (v == fa) continue;
        dfsUp(v, u);//递归到底层 
        double q = e[i].dis;
        p[u] = cup(p[u], p[v] * q);//转移 
    }
}

void dfsDown(int u, int fa) {//第二次 dfs，子树外节点传导电 
    ans += p[u];//累加答案 
    for (int v, i = head[u]; v = e[i].to, i; i = e[i].next) {
        if (v == fa) continue;
        double q = e[i].dis;
        if (fabs(p[v] * q - 1.0) < eps) {
            dfsDown(v, u);
            continue;//跳过并向下搜 
        }
        p[v] = cup(p[v], calc(p[u], p[v] * q) * q);//转移 
        dfsDown(v, u);//遍历整棵树 
    }
}

int main() {
    read(n);
    for (int i = 1; i < n; ++i) {
        int u, v;
        double w;
        read(u), read(v), read(w);
        w *= 0.01;//q%
        addEdge(u, v, w), addEdge(v, u, w);//连无向边 
    }
    for (int i = 1; i <= n; ++i) {
        read(p[i]);
        p[i] *= 0.01;//初始概率 为 节点自己充电的概率 
    }
    dfsUp(1, 0);
    dfsDown(1, 0);//根节点为 1 
    printf("%.6lf\n", ans);
    return 0;
}