「Luogu P2341」「HAOI2006」受欢迎的牛

Description

给定 $n\ (1 \leq n \leq 10^4)$ 个点，$m\ (1 \leq m \leq 5 \times 10^4)$ 条边的有向图，求有多少点能够被所有点到达（不包括自己）。

Source

Solution

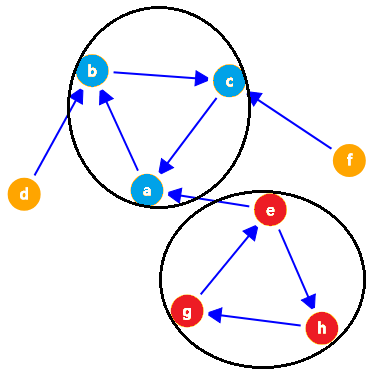
受欢迎的奶牛只有可能是出度为 $0$ 的强连通分量里的点。因为在同一个强连通分量里的所有点都是能互相到达的，所以这个强连通分量外与它相连的点不可能和这个强连通分量内的点互相到达，换句话说，如果某强连通分量内存在点 $u$，该强连通分量外某点 $v$ 与 $u$ 相连，那么边 $u \rightarrow v$ 和 $v \rightarrow u$ 只可能存在 $1$ 条，若存在边 $u \rightarrow v$（这个强连通分量的出度不为 $0$），则这个强连通分量里的点就不能被所有点到达（不存在边 $v \rightarrow u$，即 $v$ 不能到达 $u$）。如下图所示，共有 $4$ 个强连通分量，分别是 $\{a,b,c\},\{d\},\{f\},\{e,g,h\}$ 。出度为 $0$ 的强连通分量只有 $\{a,b,c\}$，这个强连通分量里的所有点都与除自己外的其它点连通。

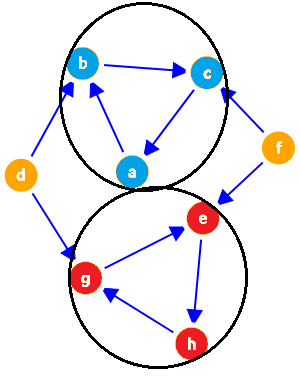
如果存在 $2$ 个及以上出度为 $0$ 的强连通分量呢（如下图）？很显然 $\{a,b,c\},\{e,g,h\}$ 这 $2$ 个强连通分量内的点彼此都不能到达，所以没有符合题意的答案。

因此跑一边 $\rm tarjan$ 缩点，把图变成一个 DAG（有向无环图至少存在一个出度为 0 的点），再统计每个强连通分量的出度，如果只存在一个出度为 $0$ 的强连通分量，那么答案就是这个强连通分量点的个数，否则答案为 $0$ 。时间复杂度为 $O(n)$ 。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

template <class T>
inline void read(T &x) {
    x = 0;
    char c = getchar();
    bool f = 0;
    for (; !isdigit(c); c = getchar()) f ^= c == '-';
    for (; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
    x = f ? -x : x;
}

template <class T>
inline void write(T x) {
    if (x < 0) {
        putchar('-');
        x = -x;
    }
    T y = 1;
	int len = 1;
    for (; y <= x / 10; y *= 10) ++len;
    for (; len; --len, x %= y, y /= 10) putchar(x / y + 48);
}

const int MAXN = 1e4, MAXM = 5e4;
int n, m, top, cnt, tot, deep, sol, ans, head[MAXN + 5], dfn[MAXN + 5], low[MAXN + 5], sta[MAXN + 5], col[MAXN + 5], size[MAXN + 5], out[MAXN + 5];
struct Edge {
    int next, to;
} e[(MAXM << 1) + 5];

inline void addEdge(int u, int v) {
    e[++tot] = (Edge) { head[u], v };
    head[u] = tot;
}

void tarjan(int u) {
    dfn[u] = low[u] = ++deep;
    sta[++top] = u;
    for (int v, i = head[u]; v = e[i].to, i; i = e[i].next) {
        if (!dfn[v]) {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        } else if (!col[v]) low[u] = min(low[u], dfn[v]);
    }
    if (dfn[u] == low[u]) {
        col[u] = ++cnt;
        for (; sta[top] != u; --top) col[sta[top]] = cnt;
        --top;
    }
}

int main() {
    read(n), read(m);
    for (int u, v, i = 1; i <= m; ++i) {
        read(u), read(v);
        addEdge(u, v);//有向边 
    }
    for (int i = 1; i <= n; ++i)
        if (!dfn[i]) tarjan(i);//缩点 
    for (int u = 1; u <= n; ++u) {
        ++size[col[u]];//统计每个强连通分量的大小 
        for (int v, i = head[u]; v = e[i].to, i; i = e[i].next)
            if (col[u] != col[v])//不在同一个强连通分量内 
                ++out[col[u]];//统计每个强连通分量的出度
    }
    for (int i = 1; i <= cnt && sol < 2; ++i)
        if (!out[i]) { 
            ans = size[i];//答案为该强连通分量的大小 
            ++sol;//出度为 0 的强连通分量个数 
        }
    write(sol > 1 ? 0 : ans);//如果不止 1 个，则无解 
    putchar('\n');
    return 0;
}