「Luogu P1627」「CQOI2009」中位数图

Description

给定长度为 $n\ (n \leq 10^5)$ 的排列，求有多少包含 $b\ (1 \leq b \leq n)$ 的奇数长度的序列中位数为 $b$ 。

Source

Solution

因为所求的是中位数，所以考虑改变原序列。把大于 $b$ 的数全部变为 $1$，小于 $b$ 的数变为 $-1$，等于 $b$ 则为 $0$ 。问题就变为求存在几个包含 $b$ 的区间和为 $0$ 。我们假设 $tmp$ 为 $b$ 的下标，原数组为 $x$，新数组为 $a$ 。

Sample Input

1 2	7 4 5 7 2 4 3 1 6

Sample Output

Example

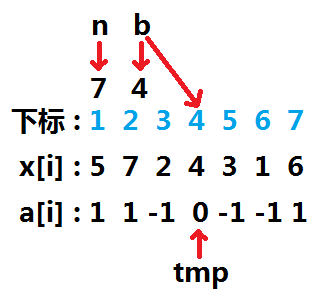
对于样例，能使结果成立的 $4$ 个区间分别为 $[1,5]$，$[1,7]$，$[2,4]$，$[4,4]$ 。

接下来我们建造两个桶，分别计数 $tmp$ 左边的后缀和与右边的前缀和，假设左边的后缀和为 $l$，右边的前缀和为 $r$ 。$l[i]/r[i]$ 表示从点 $i$ 向右/向左 到点 $tmp$ 为止 (比 $b$ 大的数的数量 - 比 $b$ 小的数的数量) 出现的次数。还是拿样例来说：

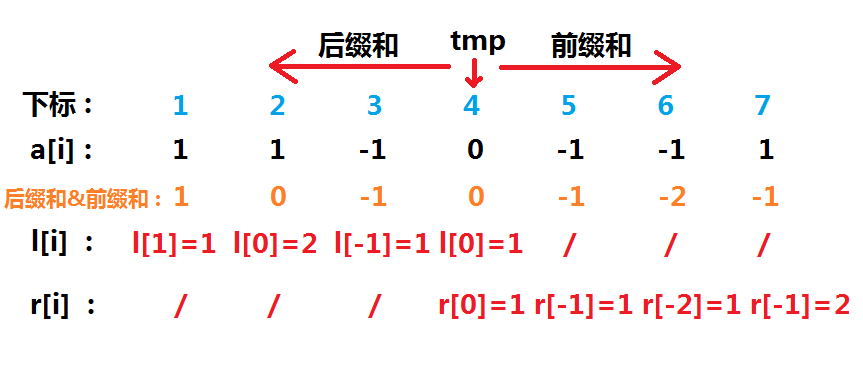
通过观察上图，我们能够发现，左边的数 $x$ 可以与右边的每一个 $-x$ 进行匹配。通过乘法原理，该值即为 $l[x] \times r[-x]$，由题意可知 $-10^5 \le x \le 10^5$，遍历所有的 $x$ 即可，最终答案为：

$\sum\limits_{i=\min{x}}^{\max{x}}l[i] \times r[-i]$

值得注意的是，$l[0]$ 和 $r[0]$ 的初始值为 $1$，因为 $b$ 是需要被算入的。当然，桶的下标不能是负数，所以我在每次操作时都加上了一个很大的数，比如数据最大值 —— $10^5$，也可以用 $\mathrm{STL}$ 中的 $map$ 解决问题，时间复杂度为 $O(n)$ 。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

template <class T>
inline void read(T &x) {
    x = 0;
    char c = getchar();
    bool f = 0;
    for (; !isdigit(c); c = getchar()) f ^= c == '-';
    for (; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
    x = f ? -x : x;
}

template <class T>
inline void write(T x) {
    if (x < 0) {
        putchar('-');
        x = -x;
    }
    T y = 1;
	int len = 1;
    for (; y <= x / 10; y *= 10) ++len;
    for (; len; --len, x %= y, y /= 10) putchar(x / y + 48);
}

const int MAXN = 1e5;
int n, b, tmp, sum, a[MAXN + 10], l[MAXN << 1 | 1], r[MAXN << 1 | 1];
LL ans;

int main() {
    read(n), read(b);
    for (int x, i = 1; i <= n; ++i) {
        read(x);
        if (x == b) tmp = i;
        else a[i] = x > b ? 1 : -1;
    }
    ++l[MAXN], ++r[MAXN];
    for (int i = tmp - 1; i >= 1; --i) {
        sum += a[i];
        ++l[sum + MAXN];
    }//后缀和
    sum = 0;
    for (int i = tmp + 1; i <= n; ++i) {
        sum += a[i];
        ++r[sum + MAXN];
    }//前缀和
    for (int i = -MAXN; i <= MAXN; ++i)
        ans += (LL) l[i + MAXN] * (LL) r[-i + MAXN];//公式计算答案
    write(ans);
    putchar('\n');
    return 0;
}