「BZOJ 1087」「SCOI2005」互不侵犯King

Description

在 $n \times n\ (1 \leq n \leq 9)$ 的棋盘上放置 $m\ (0 \leq m \leq n \times n)$ 个国王，每个国王都能攻击周围的 $8$ 个格子，求使它们无法互相攻击的方案数。

Source

[BZOJ]1087

Solution

状压DP 入门题，当然也可以打表（滑稽

如何 状态压缩？

考虑把每一行的状态用一个 二进制数 来表示。若这个数的某一位为 $1$，则代表这个位置上放了国王，$0$ 反之。

状态：

用 $f_{i,j,k}$ 表示第 $i$ 行是第 $j$ 个状态，前 $i$ 行（包括第 $i$ 行）共放了 $k$ 个国王的方案数。

初始：

$$\large {\begin{aligned} & f_{1,i,cnt_i} = 1 && \left( 当且仅当第\ i\ 个状态合法 \right) \end{aligned}}$$

其中 $cnt_i$ 表示第 $i$ 个状态国王的个数。若在第 $1$ 行状态合法，则此状态的方案数为 $1$ 。

转移：

$$\large {\begin{aligned} & f_{i,k,l} = f_{i, k, l} + f_{i - 1, j, l - cnt_k} & \left( cnt_k \leq l \leq m \right) \end{aligned}}$$

其中 $cnt_k$ 表示第 $k$ 个状态国王的个数。若第 $i - 1$ 行是 第 $j$ 个状态，第 $i$ 行是 第 $k$ 个状态，枚举 第 $j$ 个状态 和 第 $k$ 个状态，如果这两个状态合法，且 第 $k$ 个状态 能够放在 第 $j$ 个状态 的下一行（两个状态的国王保持和平），就可以转移。假设在前 $i$ 行共放了 $l$ 个国王，那么前 $i - 1$ 行就放了 $l - cnt_k$ 个国王，显然这个方案是成立的，所以累加更新这个状态的方案数。

怎么判断 两个状态合法 且 上下两行国王和平 呢？这就要用到 状态压缩 时常用的位运算了。

若第 $i$ 个状态为 $state_i$，且 $state_i\& \left( state_i << 1 \right) > 0$，则说明存在相邻的国王互相攻击，该行状态不合法。

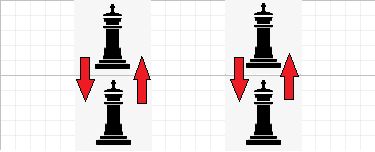
若第 $i$ 个状态为 $state_i$，第 $j$ 个状态为 $state_j$，且 $state_i\& state_j > 0 $，则说明存在上下国王互相攻击。

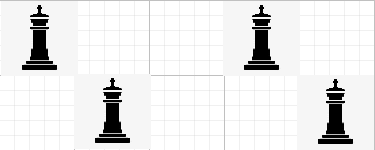
若第 $i$ 个状态为 $state_i$，第 $j$ 个状态为 $state_j$，且 $state_i\& \left(state_j << 1\right) > 0$，则说明存在左上与右下的国王互相攻击。

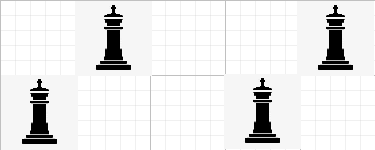
若第 $i$ 个状态为 $state_i$，第 $j$ 个状态为 $state_j$，且 $\left(state_i << 1\right) \& state_j > 0$，则说明存在右上与左下的国王互相攻击。

答案：

$$\large { \sum\limits_{i=1}^{tot} f_{n,i,m} }$$

其中 $tot$ 表示合法的状态总数。答案即为：最后一行状态合法，前 $n$ 行共放了 $m$ 个国王的方案数总和。

一行里所有的状态共 $2^n$ 个（考虑每一位是 $0$ 还是 $1$），所以时间复杂度为 $O(nm2^{2n})$，可能会超时。但很容易发现，在一行里有很多状态本来就是不合法的，比如 $n = 4$ 时 $0110$ 这个状态，实际有用的状态远不及 $2^n$ 个。因此我们考虑先用搜索预处理出所有合法的状态，再进行转移，这样效率能高很多。

Code

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;

template <class T>
inline void read(T &x) {
    x = 0;
    char c = getchar();
    bool f = 0;
    for (; !isdigit(c); c = getchar()) f ^= c == '-';
    for (; isdigit(c); c = getchar()) x = x * 10 + (c ^ 48);
    x = f ? -x : x;
}

template <class T>
inline void write(T x) {
    if (x < 0) {
        putchar('-');
        x = -x;
    }
    T y = 1;
	int len = 1;
    for (; y <= x / 10; y *= 10) ++len;
    for (; len; --len, x %= y, y /= 10) putchar(x / y + 48);
}

const int MAXN = 9, MAXM = 1 << 9;//2的9次方 
int n, m, tot, state[MAXM + 5], cnt[MAXM + 5];
LL ans, f[MAXN + 5][MAXM + 5][MAXN * MAXN + 5];

void dfs(int x, int now, int king, bool pre) {
    //x 表示已经搜到第 x 位，now 表示当前状态，king 表示当前国王数量（1 的数量），pre 表示上一位是什么 
    if (king > m) return;//国王数不能超过 m 
    if (x > n) {
        state[++tot] = now;
        cnt[tot] = king;//存下 这个状态 和 这个状态对应国王的数量 
        return;
    }
    if (!pre) dfs(x + 1, now << 1 | 1, king + 1, 1);//把 now 的第 x 位变成 1 
    //如果上一位是 1，显然这一位不能放 1 
    dfs(x + 1, now << 1, king, 0);//把 now 的第 x 位变成 0
}

int main() {
    read(n), read(m);
    dfs(1, 0, 0, 0);//预处理一行里的合法状态 
    for (int i = 1; i <= tot; ++i) f[1][i][cnt[i]] = 1;//初始 
    for (int i = 2; i <= n; ++i)
        for (int j = 1; j <= tot; ++j)
            for (int k = 1; k <= tot; ++k) {
                if ((state[j] & state[k]) || ((state[j] << 1) & state[k]) || (state[j] & (state[k] << 1))) continue;
                //判断第 k 个状态放在第 j 个状态下面一行是否合法，且不需要考虑同一行国王相邻的情况
                for (int l = cnt[k]; l <= m; ++l) f[i][k][l] += f[i - 1][j][l - cnt[k]];//转移 
            }
    for (int i = 1; i <= tot; ++i) ans += f[n][i][m];//累加放完第 n 行，共 m 个国王的所有状态 
    write(ans);
    putchar('\n');
    return 0;
}