介绍
二叉查找树(Binary Search Tree) 又称 二叉排序树(Binary Sort Tree) ,亦称 二叉搜索树,简写为 BST 。
二叉查找树具有以下性质:
- 如果左子树非空,那么左子树上的所有节点的值均小于等于根节点的值。
- 如果右子树非空,那么右子树上的所有节点的值均大于等于根节点的值。
- 二叉查找树的 左子树 与 右子树 也分别为二叉查找树。
通俗地讲:二叉查找树上点的权值,左儿子 < 根节点 < 右儿子 。
根据这个性质,我们很容易发现二叉查找树的中序遍历是一个单调不减的序列。
那么,二叉查找树有什么作用呢?
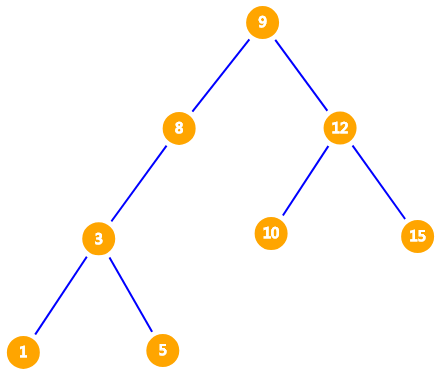
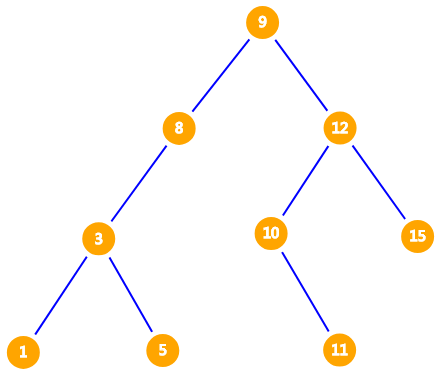
对于一个长度为 $8$ 的序列: $1, 15, 5, 3, 8, 10, 9, 12, 10$,该如何找到这个序列第 $k$ 大的数,并且支持插入与删除元素呢?如果我们将其排序再进行查询,时间复杂度为 $O(n \log n)$,这显然不够优秀。因此我们考虑构造出一棵二叉查找树,如图。
插入
假设我们要向上述序列插入一个数 $11$,我们从根节点开始。
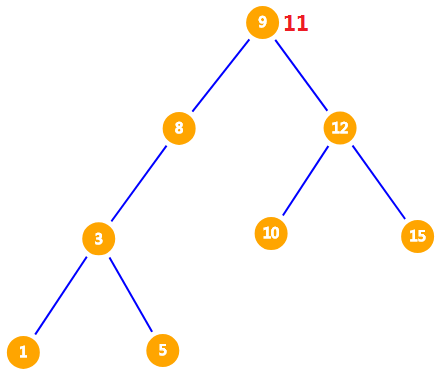
我们发现 $11 > 9$,因此我们把 $11$ 放到 $9$ 的右儿子。
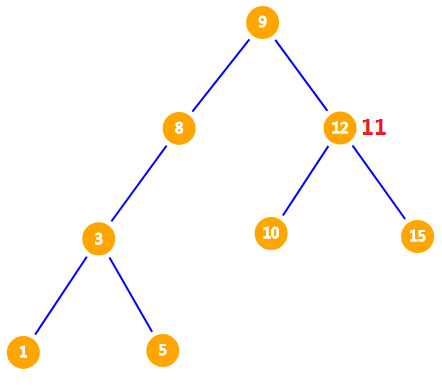
此时 $12$ 比 $11$ 大了,为了保持二叉搜索树的性质,我们把 $11$ 放到 $12$ 的左儿子。
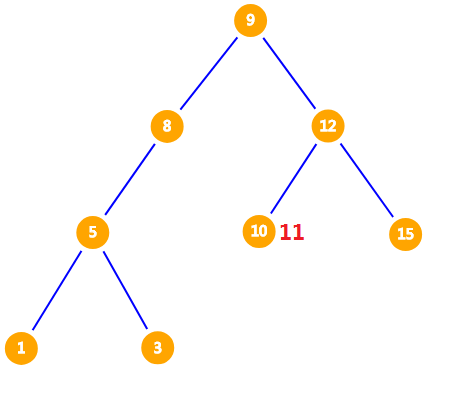
$11 > 10$,本来应该让 $11$ 和 $10$ 的右儿子继续比较,可是 $10$ 没有右儿子,因此我们把 $11$ 插入到该位置。
小结:插入一个数时,从根节点开始,依次比较要插入的数和当前节点的值,如果大于当前节点,就放到该结点的右儿子,如果小于当前节点,就放到该结点的左儿子,重复上述操作,直到下放的位置没有结点。如果中途碰到与某个节点相等,我们再定义一个 $cnt$ 数组,表示当前节点值的个数,并且加上 $1$ 。这样我们就完成了一个数的插入过程。
删除
类似插入的过程,还是依次比较要删除的数和当前节点的值,不断下放,当找到目标节点时,并不需要把该节点整个删掉,只需要给该节点值的个数减 $1$ 。对于节点 $x$,如果 $cnt[x] = 0$, 则表示当前位置没有节点。当一个位置没有节点时,这棵树依旧满足二叉查找树的性质。
查询
前驱
$x$ 的前驱定义为小于 $x$ 的最大的数。那么如何找 $x$ 的前驱呢?
这里以 $6$ 为例,从根节点开始。
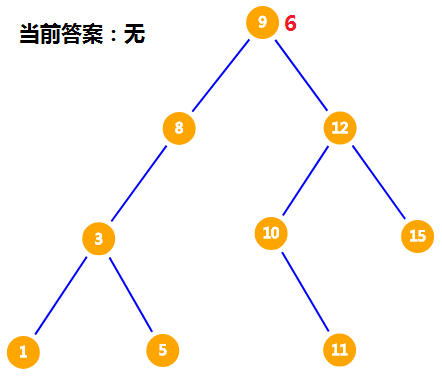
从前驱的定义可知,$6$ 的前驱一定比 $6$ 小。而 $9 > 6$,所以把 $6$ 放在 $9$ 的左儿子。
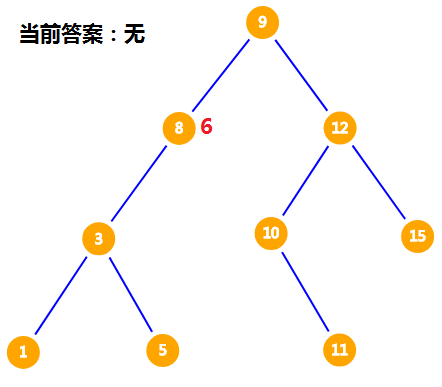
$8$ 还是比 $6$ 大,因此我们把 $6$ 放到 $8$ 的左儿子。
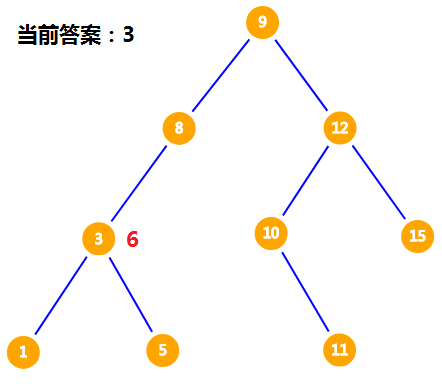
我们发现 $3 < 6$,但是并不知道 $3$ 是不是小于 $6$ 的数中最大的,我们还要去找比 $3$ 大的数,因为这些数也有可能成为答案。所以记录当前答案为 $3$,把 $6$ 放在 $3$ 的右儿子。
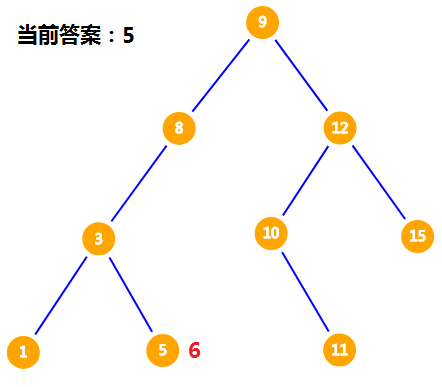
$5$ 还是比 $6$ 小,更新当前答案为 $5$,而 $5$ 没有右儿子,所以最后答案 ($6$ 的前驱)就是 $5$ 。
小结:寻找 $x$ 的前驱时,从根节点开始,依次比较 $x$ 和当前节点的值。如果当前节点的值大于 $x$,则往该节点的左儿子找,直到出现小于 $x$ 的节点。此时我们记录当前答案为这个节点的值,往这个节点的右儿子找,如果途中遇到的节点的值小于 $x$,就更新当前答案,否则结束查询,当前答案就是 $x$ 的前驱。
后继
$x$ 的后继定义为大于 $x$ 的最小的数。
与前驱的操作恰恰相反,依次比较 $x$ 和当前节点的值。如果当前节点的值小于 $x$,则往该节点的右儿子找,直到出现大于 $x$ 的节点。此时我们记录当前答案为这个节点的值,往这个节点的左儿子找,如果途中遇到的节点的值大于 $x$,就更新当前答案,否则结束查询,当前答案就是 $x$ 的后继。
已知排名求值
排名定义为比当前数小的数的个数 $+1$,现在需要寻找排名为 $x$ 的数。
我们新定义一个数组 $size$,对于一个节点 $x$,$size[x]$ 表示 $x$ 以及它的子树大小之和,需要递归预处理出每个节点的 $size$,当然,插入与删除操作时也要更新 $size$ 数组。假设我们要寻找排名为 $7$ 的数是多少,从根节点开始,如图(红色的数字即为节点的 $size$)。
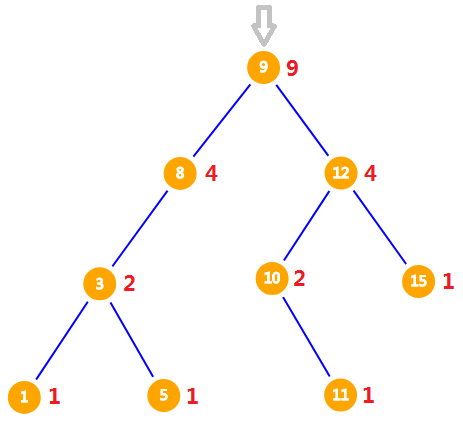
$9$ 的左儿子的 $size$ 为 $4$,所以 $9$ 的排名为 $5$,而要寻找的数的排名为 $7$,所以该数一定比 $9$ 大,因此我们到 $9$ 的右子树找。
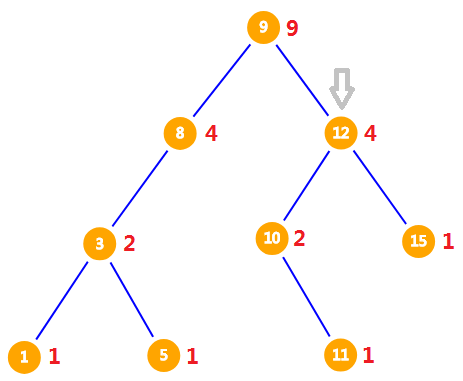
此时到了一棵新的子树上,因为排名为 $5$ 以及 $5$ 之前的节点都不要了,所以我们需要在该子树上找排名为 $2$ 的数。$12$ 的左儿子的 $size$ 为 $2$,因此 $12$ 在该子树上的排名为 $3$,排名为 $2$ 的数一定比 $12$ 小,应该到 $12$ 的左子树找。
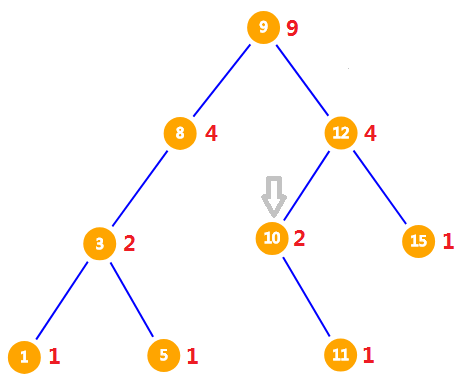
现在所在的子树又少了 $2$ 个节点,但这 $2$ 个节点的排名都比 $2$ 大,所以仍然在新子树中找排名为 $2$ 的数。因为 $10$ 没有左儿子(即 $size$ 为 $0$),所以 $10$ 的排名为 $1$,而要查询的数排名为 $2$,大于 $10$,应该到 $10$ 的右子树找。
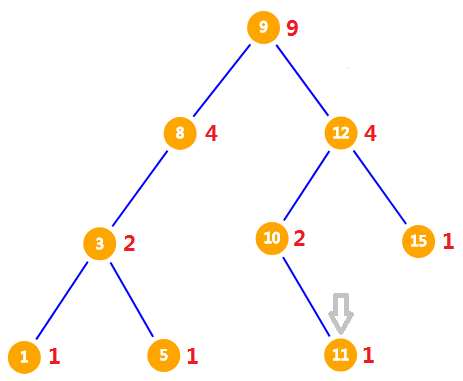
排名为 $1$ 的节点已经不要了,因此要在新子树中找排名为 $1$ 的节点。而 $11$ 没有左儿子(即 $size$ 为 $0$),所以 $11$ 的排名为 $1$ 。最后的答案就是 $11$ 。
小结:已知排名求值时,先预处理出每个节点的子树大小 $size$,从根节点开始,依次检查每个节点的排名,每个节点 $x$ 的排名为它 左儿子的 $size$ 加上 $cnt[x]$ (该节点值的数量) 。如果该节点的排名比要查询的排名小,则在该节点的右子树中查询 当前要查询的排名 - 该节点排名 的数。如果该节点排名更大,就在左子树中继续查询这个排名的数。如果排名相等,则该节点的值就是答案。
已知值求排名
与已知排名求值的过程相似,以查询 $11$ 的排名为例,从根节点开始,初始没有数比 $11$ 小,所以 $11$ 的排名为 $1$ 。

$9$ 的排名为它左儿子的 $size$ 加上它的 $cnt$,也就是 $5$,显然 $9 < 11$,所以 $11$ 的排名变为 $1 + 5 = 6$,并且往 $9$ 的右子树找。

因为 $12 > 11$,没有数比 $11$ 小,所以往 $12$ 的左子树找。

$10$ 比 $11$ 小,因为 $10$ 没有左儿子(左儿子 $size$ 为 $0$),所以 $10$ 在该子树中的排名为 $1$ 。$11$ 的排名更新为 $6 + 1 = 7$,并往 $10$ 的右子树找。

与目标节点重合,停止查询,$7$ 即为 $11$ 的排名。
小结:已知值求排名时,初始化已知值的排名为 $1$ 。从根节点开始,依次检查每个节点的值,如果该节点的值比已知值小,则排名更新为 它当前的排名 加上 该节点的排名,每个节点 $x$ 的排名为它 左儿子的 $size$ 加上 $cnt[x]$ (该节点值的数量) ,往该节点的右子树走。如果该节点的值比已知值大,则往该节点的左子树走。如果与已知值相等,则停止查询,当前排名就是这个值最终的排名。
总结
普通的二叉查找树在数据随机的情况下所有操作的时间复杂度都是 $O(\log n)$ 的,但是在最劣情况下会变成一条链,时间复杂度为 $O(n)$,因此我们需要旋转,分裂等操作来维护二叉查找树,使其时间复杂度稳定为 $O(\log n)$,这种二叉查找树称作平衡二叉树,简称平衡树。平衡树的常见实现方法有 Treap , Splay , AVL , 替罪羊树 , 红黑树 等,这里不作介绍。